Statistical Power > Matistics

What is Statistical Power?

The power of a statistical test is the probability that the test will correctly reject a false null hypothesis.
The power is defined as the probability that the test will reject the null hypothesis if the treatment has an effect.

Table of Contents.

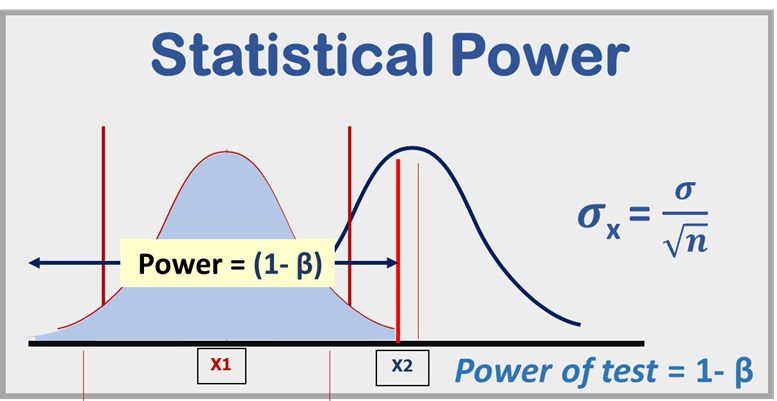
Power is the probability that the test will identify a treatment effect if its effect exists.
An alternative approach for measuring effect size is to measure the power of the statistical test.
To determine the power of a hypothesis test, you first identify the treatment and null distributions.
The power of the hypothesis test is the portion of the treatment distribution, located beyond the boundary of the critical region.
As the size of the treatment effect increases, statistical power increases. A one-tailed test has greater power than a two-tailed test.
A large sample results in more power than a small sample.

Power is calculated as a means of Power of a hypothesis test is conducted before conducting the research study to determine whether a research study is likely to be successful (reject H₀ )
Factors that influence the outcome of a hypothesis test are sample size, the size of the treatment effect, and the value chosen for the alpha level.
Whenever a treatment has an effect, there are only two possible outcomes for a hypothesis test:

A ⇒ either fail to reject H₀

B ⇒ Or reject H₀

Probability of A + Probability of B = 1

1. Failing to reject H₀ when there is a real effect, is defined as a Type II error with a probability identified as p = β.
2. Rejecting H₀ when there is a real effect, is the power of the test. Thus, the power of a hypothesis test is equal to 1 – β

Probability of A + Probability B = 1

β + Probability B = 1

Probability of B = 1- β

Power of test = 1- β

The left-hand side shows the distribution of sample means that would occur if the null hypothesis were true. The critical region is defined for this distribution.
The right-hand side shows the distribution of sample means obtained if there were an 8-point treatment effect. The sample mean is in the critical region. The probability of rejecting the null hypothesis (the power of the test) is nearly 100% for a treatment effect.

Locate the exact boundary for the critical region,
1. The critical boundary of z = +1.96 corresponds to a location, above the mean (550) by 1.96 standard deviations.
2. σ_{x =}σ / sqrt(n) = 40/5 = 8
3. Distance = 1.96 x σ_x = 1.96 x 8 = 15.68 points
4. Value at z = +1.96 is = 550 + 15.68 = 565.68
5. Any sample mean greater than 565.68 is in the critical region and will reject H₀
Find the probability value in the normal distribution table.
For the treated distribution (right-hand side), the population mean is μ = 550 and a sample mean of 570 corresponds to a z-score of 2.5

Statistical Power

p = 0.9938 or 99.38%.(from Unit Normal Table)

Statistical Power

Power and effect size are related to the treatment effect.
As the effect size increases, the distribution of sample Mean on the right-hand side moves even farther to the right so that more and more samples are beyond the z = 1.96 boundaries.
As the effect size increases, the probability of rejecting H₀ also increases, which means that the power of the test increases.
Measures of effect size such as Cohen’s d and measures of power both indicate the strength or magnitude of a treatment effect

Reducing the sample size to n = 4 has reduced the power of the test to less than 50% compared to the power of nearly 100% with a sample of n = 25.

1. Power is directly related to sample size, one of the primary reasons for computing power is to determine what sample size is necessary to achieve a reasonable probability of a successful study.
2. If the probability (power) is too small, the sample size can be increased to increase the probability (power).

Reducing the alpha level for a hypothesis test also reduces the power of the test. For example, lowering α from .05 to .01 lowers the power of the hypothesis test.

1. Using α = .05, the Boundary would be on the right-hand side z = 1.96.
2. Using α = .01 Boundary would be moved farther to the right, out to z = 2.58.

Moving the critical boundary to the right means, there would be a lower probability of rejecting the null hypothesis and a lower value for the power of the test

If the treatment effect is in the predicted direction, changing from a regular two-tailed test to a one-tailed test increases the power of the hypothesis test.
Critical region using a two-tailed test with α = .05 so that the Critical Region on the right-hand side begins at z = 1.96.
Changing to a one-tailed test would move the critical boundary to the left to a value of z = 1.65. Moving the boundary to the left would cause a larger proportion of the treatment distribution to be in the critical region and, therefore, would increase the power of the test